Introduction of Variation
Here
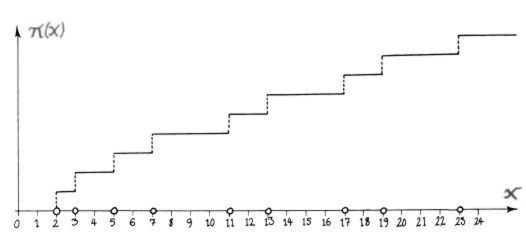
the sequence of primes is presented graphically in terms of a step function
or counting function which is traditionally denoted
p(x). (Note: this has nothing
to do with the value
p=3.14159...)
Dynamic structure of allocation of prime
numbers
in natural numbers series
is constituted by
Gaps between
consecutive
primes
Pregap Gn = Pn
– Pn -1 & postgap
gn = Pn+1 – Pn
gn º
G n+1
n – ordinal number of a
prime
After
creating the
chart of Gn
(G=f(n))
,
we see immediately in
the ocean of the apparent chaos
Islands of some regularities:

Symmetrical forms,
Symmetrical each
other forms,
And repeating
forms
!
These forms are
constituted not by gaps themselves,
But by differences
of consecutive gaps -Variations of
gaps
Vn
= g n – Gn
( Vn = G n+1 –
Gn )
Vn
=
(Pn+1
–
Pn) –
(Pn
– Pn-1) = Pn+1
–
2Pn+
Pn-1
Introduction
of
gaps
has
been the first step
of
prime numbers dynamic structure -
introduction of
VARIATIONS
is
the next, more profound, one
creating a great advantage in research of prime numbers.
It is proved to be very effective
by having discovered many unexpected regularities.

There
may be some remote analogy
between the dynamic structure
of discrete array of prime numbers
and calculus
if consider gap as Pn’
and variation as Pn”.
Both gaps (pregaps and
postgaps) and variations
involve 3 primes: Pn-1, Pn,
and Pn+1.
[ Up ] [ Introduction of Variation ] [ Regular and Repeating Groups ] [ Groups in the Range until 100,000 ] [ Groups in the Range until 1,000,000 ] [ Key of Primes Structure ] [ Distribution of gaps and variations ] [ Boolean Algebra of Classes ] [ Consecutive primes ] [ Groups of primes in the infinite set ] [ Groups of primes in a limited range ] [ We have for each kind of regular and repeating groups ]

