Distribution of gaps and variations

Distribution of gaps and variations

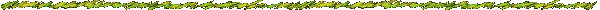
Distribution of gaps

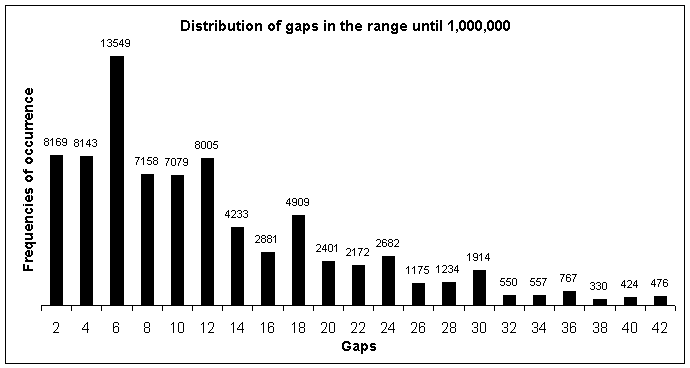
It is possible to say only that

Gaps which are multiples of 6 are more common than other gaps

and

as 'm' increases frequencies of occurence of gap values decreases.

Andrew Odlyzko, Michael Rubinstein, and Marek Wolf provide a persuative argument that the gap of 6 is the most commonly occurring, "a jumping champion", until ~1.7´10³⁶, where it changes as a jumping champion to 30, and suggest that it changes to 210 next to ~5.81´10⁴²⁸, etc.

Distribution of variations

Variations |V| ^~0 constitute major series
Variations V ⁰ constitute minor series

See also
S. Ares and M. Castro, "Hidden structure in the randomness of the prime number sequence?",
Physica A 360 (2006) 285,

P. Kumar, P. C. Ivanov and H. E. Stanley, "Information Entropy and Correlations in Prime Numbers" (2003),

Wang Liang and Huang Yan, "Pseudo Random test of prime numbers" (preprint 03/2006),

and G.G. Szpiro, "The gaps between the gaps: some patterns in the prime number sequence",
Physica A 341 (2004) 607-617

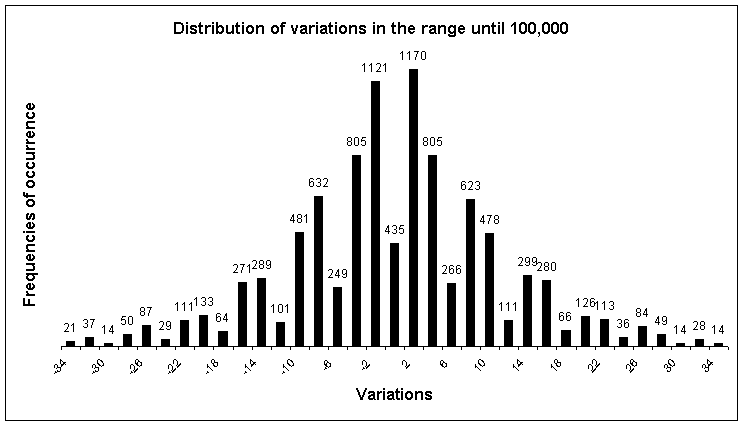
Distribution of proportions of variations' absolute values
(ratios of frequencies of occurence to the number of primes in a range)

In this chart the proportion of frequency of occurrence of V=0 has been doubled

See regressions of these distributions

Range of primes until	100,000,000	200,000,000
\|V\|^~0 constitute series	0.196e ^{- 0.071\| V \|}	0.172e ^{- 0.067\| V \|}
\|V\| ⁰ constitute series	0.079e ^{- 0.071\| V \|}	0.069e ^{- 0.067\| V \|}
M/m	2.474	2.498

|K | = 1 for V ^~0 and |K| = 0 for V ⁰

^so

Y ≈ M(M/m) ^|K|-1 e ^- ^b|V|

In the infinite general set of primes
what consecutive primes of any class appear independently in

M/m → 3/2

^{The
rule of the distribution of variations'
absolute values is much stricter (and
more beautiful) than
one of gaps values, and
the significance of key number}6 is much more obvious!

What is the reson of six period oscillations in these histograms?

It is the probabilities of groups of two and three consecutive primes of the same class
constituting gaps and variations multiple of 6.

For the infinite general primes' set,
The probability of being the next prime of the class of the previous one is equal ½.
So, probability of being gaps multiple of 6 is ½.
The ratio of the number of P⁺ to the number of P^- in the range until 100,000,000 is equal p⁺/ p^-= 1.00015 ≈1,
therefore G⁺(P_n⁺-P_{n
-1}^-)and G^-(P_n^- - P_{n
-1}⁺) have almost equal probabities of occurrence, too, i.e. ¼ per each a class.
So, G⁰ are more common than G⁺ or G^-.

Accordingly, the probability of being the three consecutive primes of the same class is equal (½)².
Therefore, probability of being variations multiple is ¼, and probability of being V⁺or V^-is 3/8.
So, V⁰ are less common than V⁺ or V^-.

^{6666666666666666666666666}

^{As the range of primes increases,
'm' and 'b' decrease}

See Variations Distribution

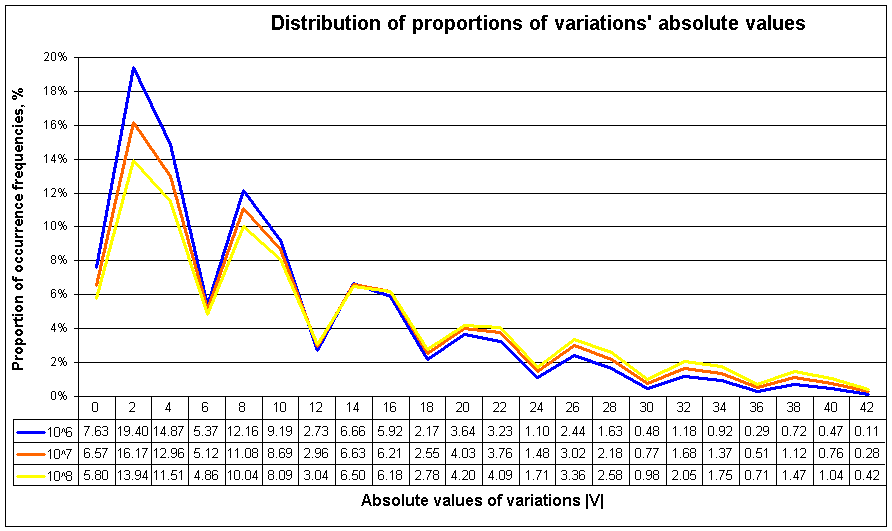
Because of that, a suspicion of the possibility of turning the slope horizontal and even going upward arises.

It means to be similar to the change of "jumping champion".

[ Up ] [ Introduction of Variation ] [ Regular and Repeating Groups ] [ Groups in the Range until 100,000 ] [ Groups in the Range until 1,000,000 ] [ Key of Primes Structure ] [ Distribution of gaps and variations ] [ Boolean Algebra of Classes ] [ Consecutive primes ] [ Groups of primes in the infinite set ] [ Groups of primes in a limited range ] [ We have for each kind of regular and repeating groups ]