Consecutive primes

The assumption that consecutive primes can be of any classes, P=6n+1 and P=6n-1, independently only because they are equally likely creates the probability of being both of consecutive primes of the same class(having the gap between them multiple of 6) equal 1/2 (Ares, Saul, and Mario Castro. Hidden structure in the randomness of the prime number sequence. arXiv:cond-mat/0310148 v1 7 Oct 2003
http://www.mpipks-dresden.mpg.de/$\sim$ saul/papers/primes.pdf ).

It is of very important role that all primes are distributed in groups of the same class beginning from the size equal 1 (singles) to maximal one in a range of primes. In the range until 100,000,000, the maximal size of such groups is equal 16. This size increases when increases a range, and a number of primes in a groups of bigger size is less than a number of them in a groups of smaller size.

Groups of the same class create inside them differences of consecutive primes multiple of 6. The first differences, gaps, G⁰ exist inside groups of the size more than 1 (nonsingles). The second differenses, variations, V⁰ do inside groups of a size more than 2.

Theory

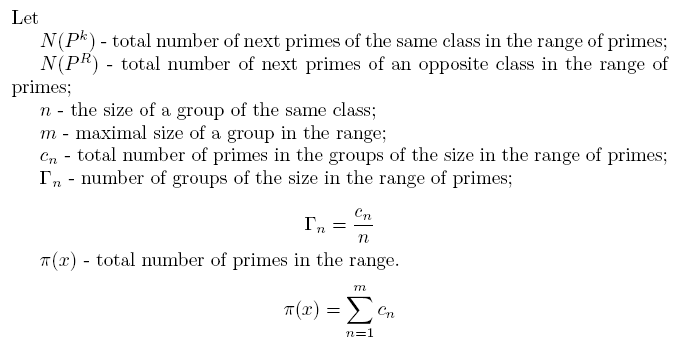
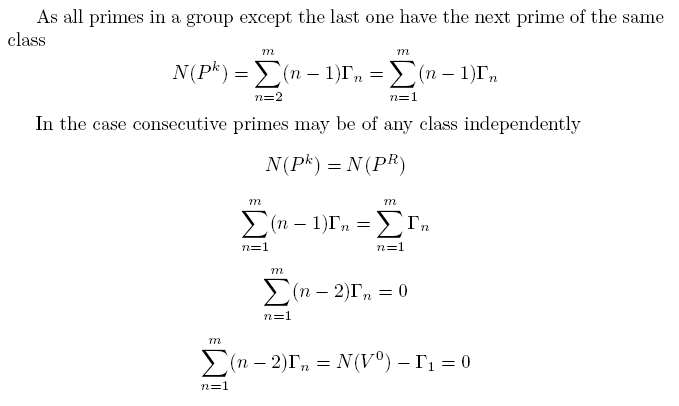
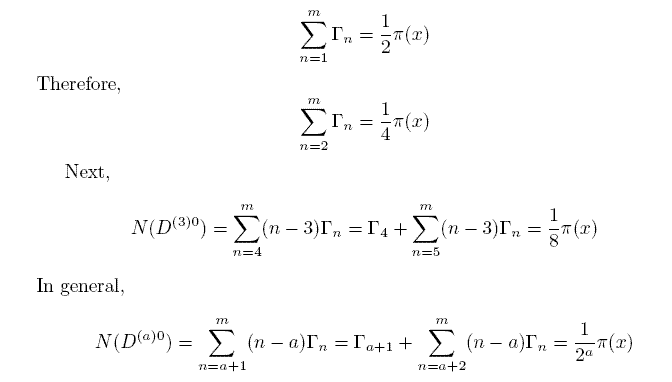
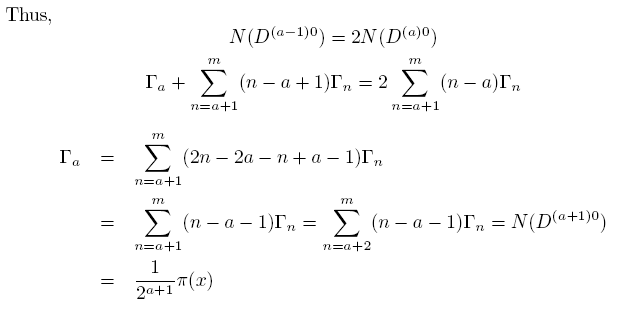
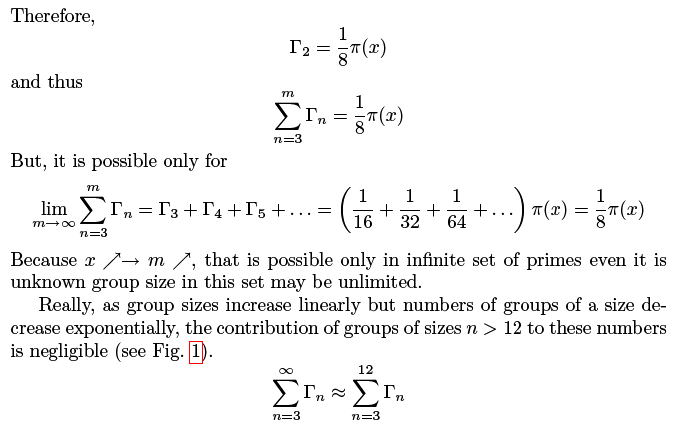
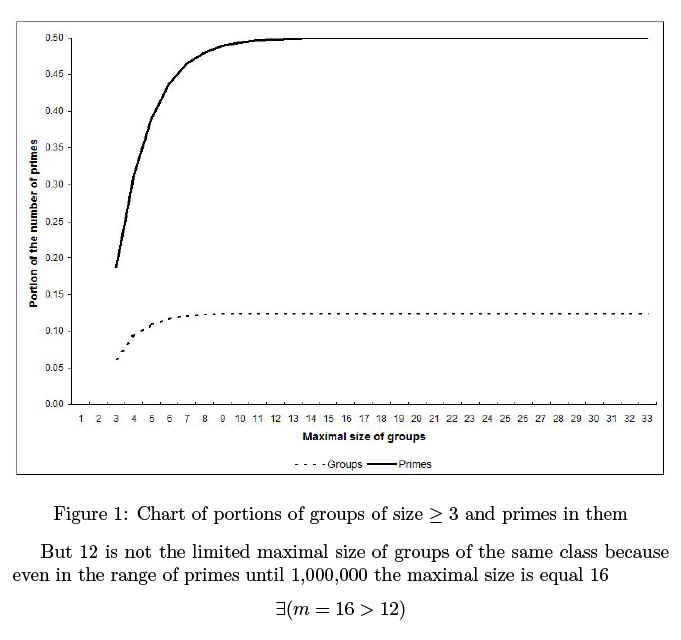
Thus, appearing of consecutive primes of any class independntly is possible when x= ¥ (m=¥) , i.e. for the infinite general primes' set only. The condition N(P^k)=N(P^R)=½p(x) approaches to true as x®¥ but reaches it never.