Regular and Repeating Groups

Regular and Repeating Groups

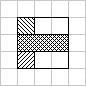
Groups are constituted by consecutive variations.

The size of the group is the number of variations in it
(except for flats - groups of equal gaps).

All regular groups have symmetry, axial or polar.

Symmetrical groups having any variations:

symmetriads having a horisontal axis of symmetry,

curls                having polar symmetry;

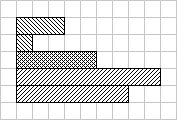
Special groups

stairs having equal variations
(a special kind of curls);

zigzags    having the same absolute values and alternating   signs of consecutive variations
(a special kind of even symmetriades or odd curls);

                and flats having only variations equal zero,
                               and which size of is the number of consecutive constant gaps in it
                               (a special kind of all previous kinds of regular groups).



Repeating groups constitute clusters of 3 kinds: levels, pairs, and foursomes.

Flats having the same gaps                                                                         constitute levels.

Uniform symmetriads , curls, stairs , and zigzags,
               having vertical symmetry each to other,                                         constitute pairs.

Uniform repeating irregular groups
having both vertical and horizontal symmetry each to other do foursomes.

REGULAR GROUPS
in the range until 1,000,000,000

FLATS
V = 0
have 2, 3, 4, and 5 gaps
The consecutive equal gaps are repeating elements,
and the size is the number of consecutive gaps
Maximal size = 5
G_n Î G⁰

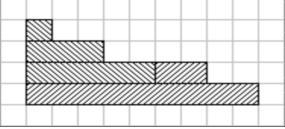
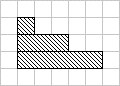
STAIRS
V_i = V_i+1
have 2, 3, 4, 5, 6, 7, 8, and 9 variations

Maximal size = 9

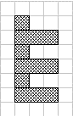
ZIGZAGS
V_i = - V_i+1
have 3, 4, 5, and 6 variations

Maximal size = 6

SYMMETRIADS
G_{c - i}= G_{c + i}

Evensymmetiads
V_{c - i} = - V_{c + i- 1} have 2, 4, 6, 8, 10,

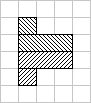
Oddsymmetriads
V_c = 0
V_{c - i} = - V_{c + i} have 3, 5, and 7 variations
Maximal size = 7
G_c Ì G⁰G_cG_nÎ G⁰      GV_nÎ V ⁰G⁰G_c Ì G⁰

CURLS

Evencurls
G_c - G_{c - i} = G_{c + 1}- G_cV_{c - i} = V_{c + i}-₁
have 4, 6, 8, and 10 variations
Maximal size = 10

Oddcurls
V_{c - i} = V_{c + i}
have 3, 5, 7, 9, 11, and 13 variations

Maximal size = 13

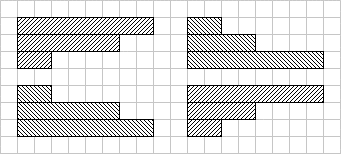
FOURSOMES

Irregular repeating groups constituting a foursome have the same set of variations
and are of four kinds:

    groups having the sequence of variations downward:
                   - positive groups (main kind);
                   - negative groups having the same variations with the reversed sign;

   antigroups having the reversed order of the sequence of variations (upward):
                   - positive antigroups having the same variations with the reversed sign;
                   - negative antigroups having the same variations with the same sign.

Negative group
Positive group

Negative antigroup
Positive antigroup

Maximal size of each type of regular or irregular repeating groups
depends on its dynamic characteristics .

Some maximal groups may be unique