Groups of primes in a limited range
![]()
In the range until 1,000,000
The ratio of the number of P+ to the number of P- in this range is equal p+/ p-= 1.00015 ≈1.
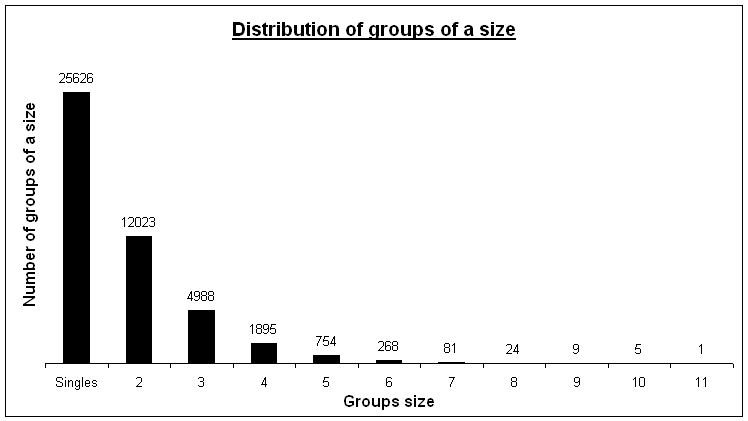
Unlike
in
the
infinite
general
set,
every
ratio
of
a
number
of
groups
of
next
bigger
size
to
that
of
groups
of
previous
size
is
less
than
2,
and
it
increases
when
the
sizes
of
groups
increase.
The only 11-group contains P+.
| Ord# | P | Pmod6 | ||
| 34368 | 406907 | 5 | ||
| 34369 | 406951 | 1 | ||
| 34370 | 406969 | 1 | ||
| 34371 | 406981 | 1 | ||
| 34372 | 406993 | 1 | ||
| 34373 | 407023 | 1 | ||
| 34374 | 407047 | 1 | ||
| 34375 | 407059 | 1 | ||
| 34376 | 407083 | 1 | ||
| 34377 | 407119 | 1 | ||
| 34378 | 407137 | 1 | ||
| 34379 | 407149 | 1 | ||
| 34380 | 407153 | 5 | ||
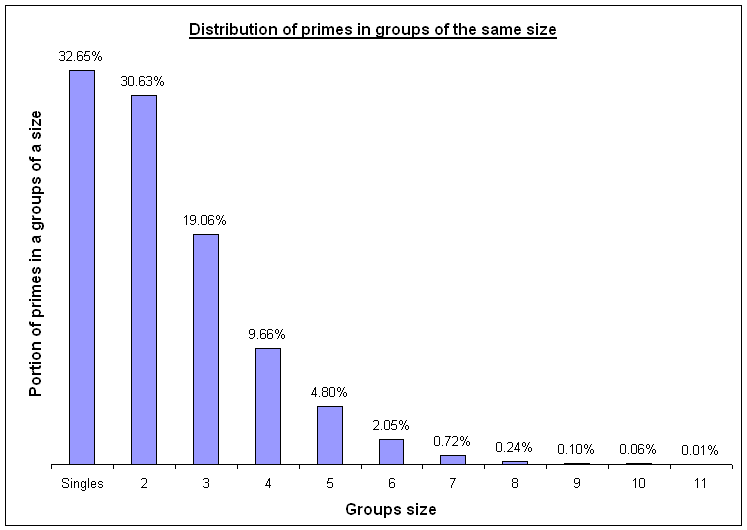
Thus,
~1/3
primes
of
a
class
go
single
(more
than
in
the
infinite
general
set),
~1/3
ones
go
in
pairs
(more
than
in
the
infinite
general
set),
and
~1/3
ones go in groups of size >
2
(less
than
in
the
infinite
general
set).
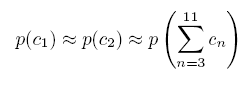
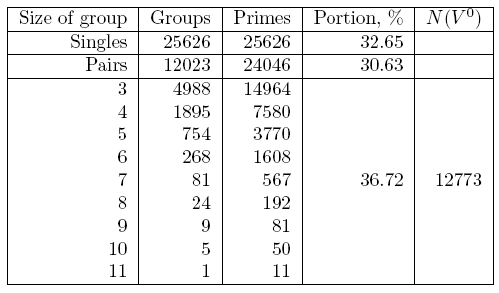
~1/6 go inside groups of more than 2 consecutive Pk (have V0);
~1/2 of Pk appear as the first or last members of nonsingle groups of consecutivePk,
and ~1/2 of them have an ajacent single PR (found by sorting primes by class).
N(V0) » 1/6 p(x) » ½ c1
Additionally, it is possible to consider the portions of V + and V- are equal, so each of them is 5/12, and the ratio of such a portion to the portion of V 0 is equal approximately (5/12)/(1/6) = 5/2 = 2.5. But, the ratio M/m for regressions of distribution of absolute values of variations in the range until 200,000,000 is equal 2.498 ≈ 2.5, too!
Let's research this analytically and check numerically
Because only last members of groups have the next prime of an opposite class
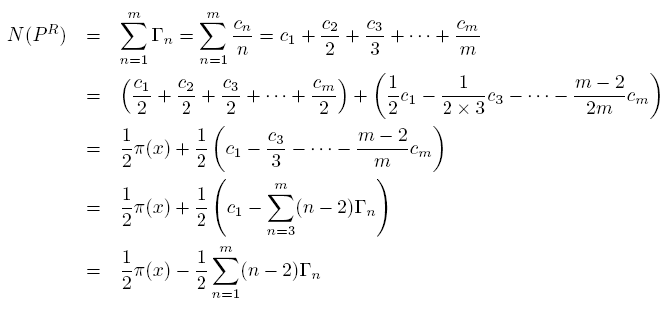
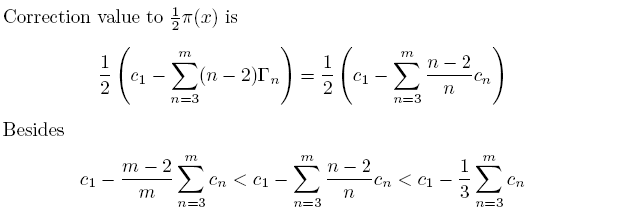
For this range
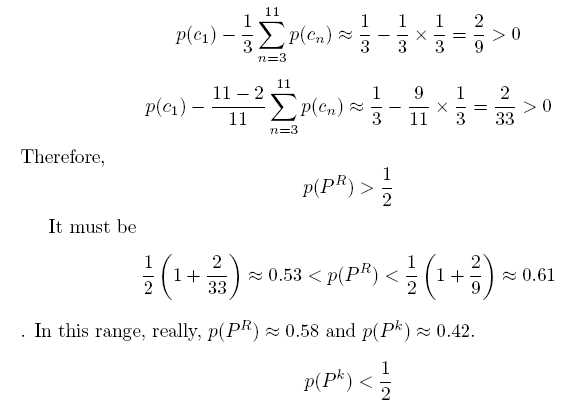
The reason of different condition in a finite set of primes is hidden in real primes' distribution in groups of the same class.
Singles create next primes of an opposite class only (both gaps and variations, not multiple of 6 only).
Pairs do equal numbers of next primes of both the classes (equal numbers of gaps multiple of 6 and not; and variations not multiple of 6, only) .
And groups of n > 2 create more next primes of the same class than ones of an opposite class (more gaps , multiple of 6, than not; and variations multiple of 6 for all inner primes of groups).
The predominance of the role of singles over the role of primes in groups of sizes more than 2
(maximally
trice)
is a reason of being
p(Pk)
<
½ in a finite set of primes.
666666666666
Maximal groups of primes of the same class
In the range until 10,000,000
The only 13-group contains P+.
In the range until 35,000,000
The only 15-group contains P-.
In the range until 100,000,000
Two 16-groups contain P+.